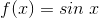Dropdown Menu

[Matemáticas Aplicadas] 3. Funciones

ÍNDICE
  • Funciones
    • Dominio
    • Codominio
    • Imagen
    • Tipos de funciones
      • Función inyectiva
      • Función epiyectiva
      • Función biyectiva
  • Función lineal
  • Función cuadrática
  • Función exponencial
  • Función logarítmica
  • Funciones trigonométricas
    • Función Seno
    • Función Coseno
    • Función Tangente
  • Función raíz
  • Función potencial
  • Función polinómica
  • Función racional


FUNCIONES

El concepto de función se refiere a una regla o algoritmo que asigna a cada elemento de un conjunto X un único elemento de un segundo conjunto Y.

Por ejemplo, el conjunto X podría ser un conjunto de nombres (Carlos, Ana...) y el conjunto Y las letras del abecedario (A, B, C, D, E...). Así, para cada nombre del conjunto X tendríamos una única inicial dentro del conjunto Y (Carlos → C, Ana → A...), por lo que la función f sería la regla o algoritmo que deberíamos aplicar para sacar el valor único del conjunto Y dado el valor del conjunto X.


El dominio de la función es el conjunto de valores que puede tomar x, es decir, los valores del conjunto X.

El codominio de la función es el conjunto de valores sobre el que se aplica la función para obtener el valor y, es decir, los valores del conjunto Y.

La imagen de la función es el conjunto de valores que puede tomar f(x), es decir, los valores del conjunto Y una vez aplicada la función.

Podemos establecer la siguiente clasificación básica de las funciones:
  • Función Inyectiva: Una función inyectiva (o función uno a uno) es aquella en la que para cada elemento del dominio le corresponde un único elemento del codominio, pero no a la inversa.
  • Función Epiyectiva: Una función epiyectiva es aquella en la que todos los elementos del codominio son imagen de, al menos, un elemento del dominio; en otras palabras, si todos valor de Y se corresponde con algún valor de X.
  • Función Biyectiva: Una función biyectiva es aquella que es inyectiva y epiyectiva a la vez, es decir, que cada valor del dominio se corresponde con un único valor del codominio.


FUNCIÓN LINEAL

Una función lineal es aquella representada por una línea recta en el plano cartesiano. Por tanto, su función será la ecuación punto-pendiente que vimos en el apartado de Geometría Analítica.


Si m = 0, la función será constante.
Si m < 0, la función será decreciente.
Si m > 0, la función será creciente.


FUNCIÓN CUADRÁTICA

La función cuadrática está representada por una parábola vertical.


Como se puede observar, se trata de una ecuación de segundo grado, cuya resolución es la siguiente:



Si a < 0, la parábola está orientada hacia abajo
Si a > 0, la parábola está orientada hacia arriba


FUNCIÓN EXPONENCIAL

La función exponencial está representada por una curva sobre el eje X.


Si a > 1, la función es creciente.
- Si x > 0, la función siempre es > 1.
- Si x < 0, la función siempre está entre [0, 1].
Si 0 < a < 1, la función es decreciente.
- Si x > 0, la función siempre está entre [0, 1].
- Si x < 0, la función siempre es > 1.

Si a = 1, la función se convierte en una función lineal.

Si a < 0, la función se invierte en el eje X.








FUNCIÓN LOGARÍTMICA

La función logarítmica está representada por una curva sobre el eje Y.


Si a < 1, la función es creciente.
Si 0 < a < 1, la función es decreciente.
Si x = 1, la función siempre vale 0.

El crecimiento de estas funciones es menor que el crecimiento de las funciones exponenciales.


FUNCIONES TRIGONOMÉTRICAS

Las funciones trigonométricas pueden ser definidas a través de la circunferencia unitaria (radio = 1), centrada en el origen.
La función seno tiene un recorrido de -1 a 1, siendo periódica con período en 2π.
La función coseno tiene un recorrido de -1 a 1, siendo periódica con período en 2π.

La función tangente tiene un recorrido de todos los números reales (ℝ), siendo periódica con período en π.




FUNCIÓN RAÍZ





FUNCIÓN POTENCIAL





FUNCIÓN POLINÓMICA





FUNCIÓN RACIONAL





BIBLIOGRAFÍA Y WEBGRAFÍA


TOOLS
Etiquetas: